はじめに
画像処理は、デジタル画像を操作してその内容を解析、変換、編集する技術です。この技術は、写真編集、医療画像解析、自動運転車の視覚システムなど、さまざまな分野で利用されています。このシリーズは、実際の画像処理技術をPythonで実装することで、理論と実践を組み合わせた学習を目指しています。画像処理の分野でよく使用される手法に「大津の二値化」と「HSV変換」があります。これらの手法は、画像の特定の特徴を強調したり、色情報を効果的に利用したりするために非常に有用です。本記事では、これらの手法について詳細に解説し、Pythonの標準ライブラリのみを使ってそれらを実装する方法を示します。この記事では、画像処理100本ノックで用意されている「imori.jpg」をダウンロードしてください。ダウンロードのURLはこちらです。
画像処理100本ノック 004. 大津の二値化
大津の二値化を実装せよ。 大津の二値化とは判別分析法と呼ばれ、二値化における分離の閾値を自動決定する手法である。 これはクラス内分散とクラス間分散の比から計算される。
画像処理100本ノック
方針
大津の二値化(Otsu’s method)は、1979年に大津健一によって提案された自動二値化手法です。この方法は、画像のヒストグラムを解析し、二つのクラス(背景と前景)の間の分離の最適な閾値を自動的に決定します。ここで重要なのは、画像中のピクセルの分布に基づいて最適な閾値を見つける点です。これにより、手動で閾値を設定する必要がなくなり、異なる画像に対しても適用可能な汎用的な手法となっています。
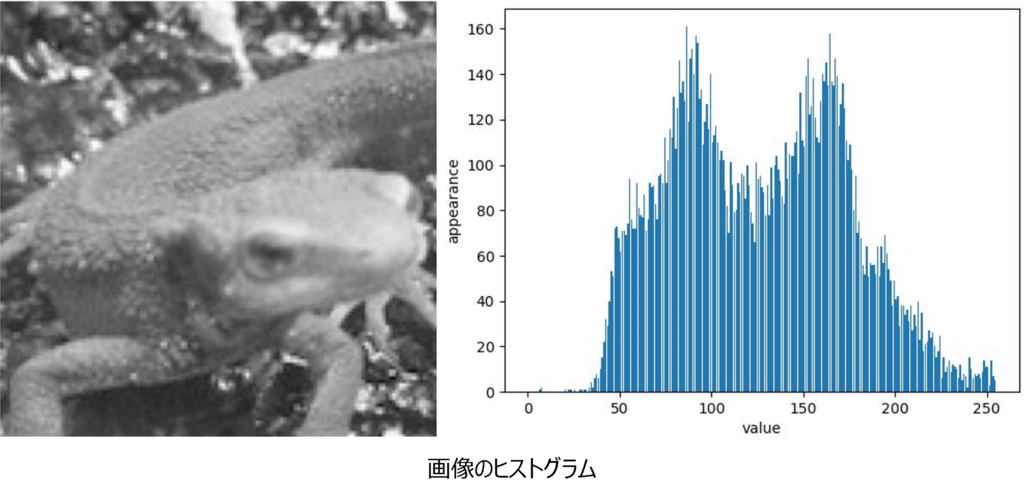
大津の二値化の基本的なアイデアは、クラス内分散(within-class variance)とクラス間分散(between-class variance)の比を最大化することです。画像の輝度値のヒストグラムを基に、各ピクセルの輝度値を背景と前景の二つのクラスに分け、それぞれのクラス内の分散を計算します。クラス内分散は各クラスのピクセルの輝度値のばらつきを表し、クラス間分散は二つのクラス間の輝度値の差を表します。
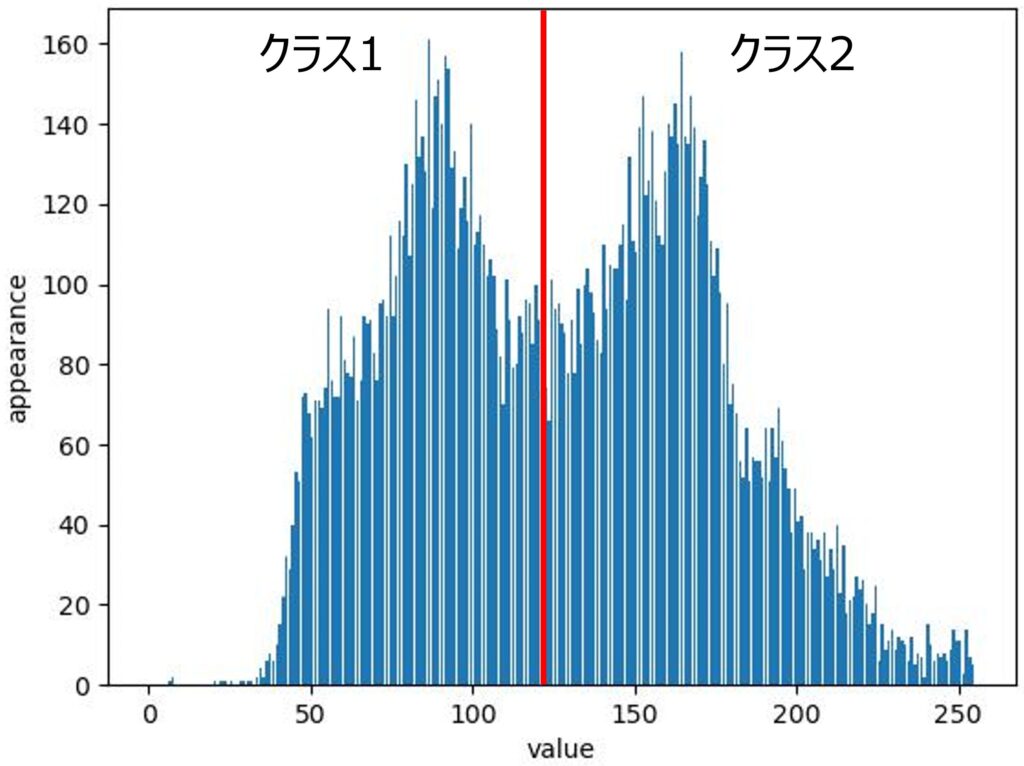
まず、画像全体の輝度値のヒストグラムを計算します。次に、各閾値に対して、背景と前景の二つのクラスに分け、それぞれのクラスの平均輝度値を求めます。その後、各クラスの重み(ピクセル数の割合)を計算し、クラス内分散とクラス間分散を求めます。最後に、クラス間分散が最大となる閾値を最適閾値として選定します。
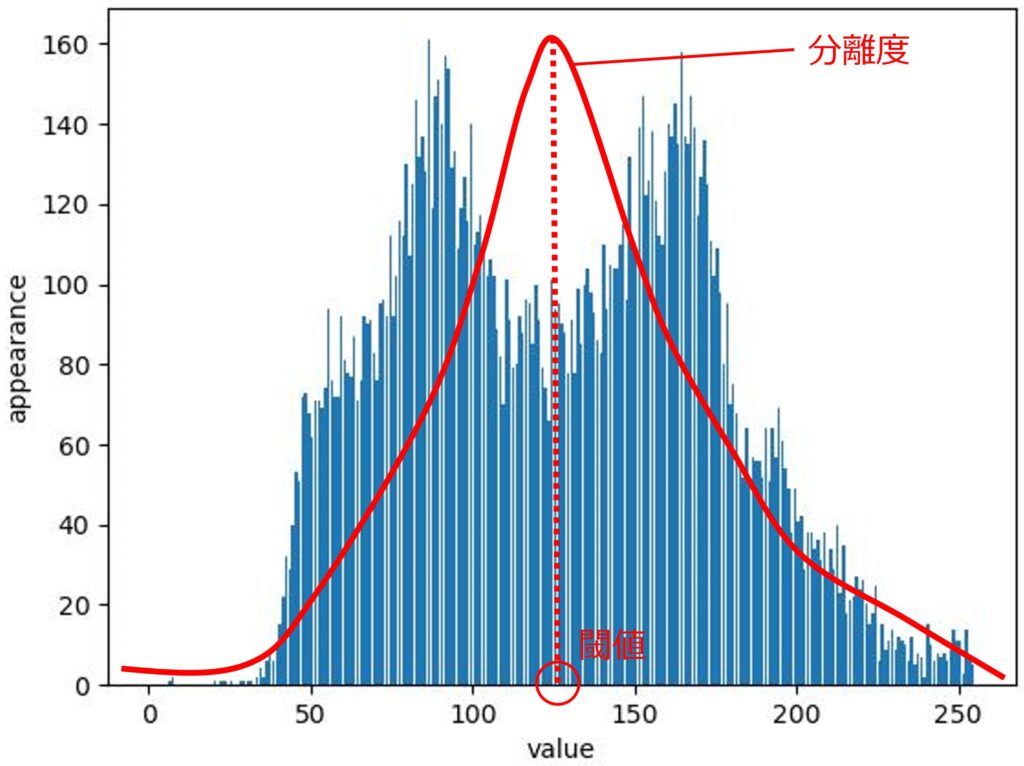
数式で表すと、まず各輝度値 t に対して背景クラス C1 と前景クラス C2 に分け、各クラスの平均輝度値 μ1(t) と μ2(t) を求めます。クラスの重み w1(t) と w2(t) は次のように計算されます。
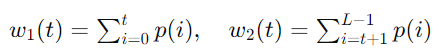
ここで、 p(i) は輝度値 i の出現頻度です。クラスの平均輝度値 μ1(t) と μ2(t) は次のように計算されます。
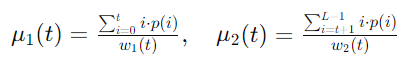
クラス間分散 σB2(t) は次のように計算されます。
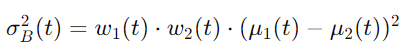
このクラス間分散 σB2(t) が最大となる t を最適閾値とします。
実装手順
- ヒストグラムの作成:
- 画像の各画素の輝度値(0-255)の分布を計算します。
- 累積分布関数の計算:
- 各輝度値の出現頻度を累積的に計算します。
- クラス内分散の計算:
- 各閾値ごとにクラス内分散を計算します。
- クラス間分散の計算:
- 各閾値ごとにクラス間分散を計算します。
- 判別分析の最適化:
- クラス内分散とクラス間分散の比が最大になる閾値を選定します。
解答と実行結果
まず入力画像をグレースケールに変換し、その後、輝度値のヒストグラムを計算します。次に、各閾値に対してクラス内分散とクラス間分散を計算し、最大の判別分析結果を得る閾値を決定します。最後に、その閾値を使用して画像を二値化します。
import cv2
import numpy as np
def otsu_binarization(image):
# グレースケール化
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# ヒストグラムの計算
histogram = np.bincount(gray.flatten(), minlength=256)
# 画素数の合計
total = gray.size
current_max, threshold = 0, 0
sumB, sum1 = 0, np.dot(np.arange(256), histogram)
wB, wF = 0, 0
for i in range(256):
wB += histogram[i]
if wB == 0:
continue
wF = total - wB
if wF == 0:
break
sumB += i * histogram[i]
mB = sumB / wB
mF = (sum1 - sumB) / wF
between = wB * wF * (mB - mF) ** 2
if between > current_max:
current_max = between
threshold = i
# 二値化
binary_image = gray.copy()
binary_image[gray > threshold] = 255
binary_image[gray <= threshold] = 0
return binary_image
# 画像の読み込み
image = cv2.imread('imori.jpg')
binary_image = otsu_binarization(image)
cv2.imwrite('binary_image.jpg', binary_image)このコードを実行すると、次のような結果(右の画像)が得られます。

画像処理100本ノック 005. HSV変換
HSV変換を実装して、色相Hを反転せよ。HSV変換とは、Hue(色相)、Saturation(彩度)、Value(明度) で色を表現する手法である。
画像処理100本ノック
方針
HSV(Hue, Saturation, Value)色空間は、RGB色空間とは異なる色の表現方法です。各成分の意味は以下の通りです。
- Hue(色相): 色の種類を示す値。0-360度の範囲で表され、0度が赤、120度が緑、240度が青を表します。
- Saturation(彩度): 色の鮮やかさを示す値。0-1の範囲で表され、0は無彩色(グレー)、1は純色を表します。
- Value(明度): 色の明るさを示す値。0-1の範囲で表され、0は黒、1は最大の明るさを表します。
RGB色空間は、画像の色を赤(Red)、緑(Green)、青(Blue)の三つの成分で表現します。一方、HSV色空間は、色相(Hue)、彩度(Saturation)、明度(Value)の三つの成分で色を表現します。この変換は、色の直感的な操作を可能にします。たとえば、特定の色相を変えたり、彩度や明度を調整することで、画像全体の色調を変更できます。RGBからHSVへの変換は、まずRGB値を正規化して0から1の範囲にします。その後、以下の手順で各成分を計算します。
- 明度 V は R、G、B の最大値です。
- 彩度 S は最大値と最小値の差を最大値で割った値です(ただし、最大値が0の場合は0になります)。
- 色相 H は最大値に応じて計算されます。最大値が R の場合、G と B の差を最大値と最小値の差で割って計算し、360度の範囲に変換します。最大値が G や B の場合も同様に計算されます。
具体的な数式は以下の通りです:
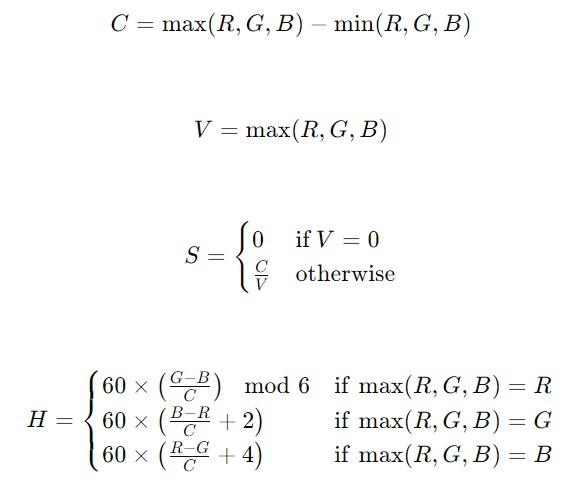
実装手順
HSVからRGBへの変換は、まず色相 H を基にRGB値を計算します。色相は0から360度の範囲で表され、彩度 S と明度 V を使用してRGB値を調整します。具体的な手順は以下の通りです:
- RGB画像を読み込む:
- 画像を読み込み、各ピクセルのRGB値を取得します。
- RGBからHSVへの変換:
- 各ピクセルのRGB値をHSV値に変換します。
- 色相の反転:
- 色相成分を180度反転させます。
- HSVからRGBへの再変換:
- 反転したHSV値をRGB値に再変換します。
解答と実行結果
まず入力画像をHSV色空間に変換し、色相(H)成分を180度反転させます。その後、反転後のHSV値を再びRGB色空間に変換して、色相を反転させた画像を生成します。
import cv2
import numpy as np
def rgb_to_hsv(image):
image = image.astype(float) / 255.0
R, G, B = image[..., 0], image[..., 1], image[..., 2]
M = np.max(image, axis=-1)
m = np.min(image, axis[-1])
C = M - m
H = np.zeros_like(M)
S = np.zeros_like(M)
V = M
mask = C != 0
S[mask] = C[mask] / M[mask]
mask_r = (M == R) & mask
mask_g = (M == G) & mask
mask_b = (M == B) & mask
H[mask_r] = (G[mask_r] - B[mask_r]) / C[mask_r] % 6
H[mask_g] = (B[mask_g] - R[mask_g]) / C[mask_g] + 2
H[mask_b] = (R[mask_b] - G[mask_b]) / C[mask_b] + 4
H *= 60
H[H < 0] += 360
return np.stack([H, S, V], axis=-1)
def hsv_to_rgb(hsv_image):
H, S, V = hsv_image[..., 0], hsv_image[..., 1], hsv_image[..., 2]
C = V * S
X = C * (1 - np.abs(H / 60 % 2 - 1))
m = V - C
rgb_image = np.zeros_like(hsv_image)
h0, h1, h2 = H < 60, (60 <= H) & (H < 120), (120 <= H) & (H < 180)
h3, h4, h5 = (180 <= H) & (H < 240), (240 <= H) & (H < 300), H >= 300
rgb_image[h0] = np.stack([C, X, 0], axis=-1)[h0]
rgb_image[h1] = np.stack([X, C, 0], axis[-1])[h1]
rgb_image[h2] = np.stack([0, C, X], axis[-1])[h2]
rgb_image[h3] = np.stack([0, X, C], axis[-1])[h3]
rgb_image[h4] = np.stack([X, 0, C], axis[-1])[h4]
rgb_image[h5] = np.stack([C, 0, X], axis[-1])[h5]
return (rgb_image + m[..., np.newaxis]) * 255
def hsv_inversion(image):
hsv_image = rgb_to_hsv(image)
hsv_image[..., 0] = (hsv_image[..., 0] + 180) % 360
return hsv_to_rgb(hsv_image).astype(np.uint8)
# 画像の読み込み
image = cv2.imread('imori.jpg')
inverted_image = hsv_inversion(image)
cv2.imwrite('inverted_image.jpg', inverted_image)このコードを実行すると、次のような結果(右の画像)が得られます。

最後に
大津の二値化とHSV変換は、画像処理において非常に強力な手法です。これらの手法を理解し、実装することで、画像処理の基礎を深く理解することができます。次回も引き続き、画像処理の基本的な手法について学んでいきましょう。
私の経歴などについては以下の記事から確認することができます!
ブログランキングに参加しています。ぜひクリックで応援お願いします



コメント